
3èmes - Lundi 25 mai ~ mardi 26 mai: représentation d'une fonction linéaire
Résumé de la séance:
- déterminer une fonction linéaire à partir de sa droite représentative
- confirmer une lecture graphique par calcul
- découverte des fonctions affines
Pour commencer, on peut remarquer que toutes les courbes proposées sont des droites passant par l'origine. Elles correspondent donc bien à des fonctions linéaires. Par calcul, on voit clairement que: Ces conclusions pourraient aussi être tirées de l'observation de l'image de 1 pour chaque courbe ou du calcul de la pente entre deux points d'une droite (mais nous verrons ça plus tard). 1. a. L'image de 4 par la fonction \(g\) est 2. b. 1 a 2 pour antécédent par la fonction \(g\). Quelque soit la méthode, on trouve que \(g:x\mapsto \frac{1}{2}x\) \(g(9)=\frac{1}{2}\times 9 = \frac{9}{2}\) L'image de 9 par \(g\) est 4,5. Correction
9 p123: trouver l'expression d'une fonction linéaire à partir de sa droite représentative
De même, les 3 fonctions proposées sont bien des fonctions linéaires (toutes avec une expression de la forme \(x \mapsto ax\)).
On peut procéder par calcul, par lecture directe ou par élimination.
Commençons par comparer les droites:
11 p123: même chose avec en plus des questions de lecture graphique
(le 4 se trouve sur l'axe des abscisse, on "va jusqu'à la droite puis jusqu'à l'axe des ordonnées" pour trouver 2)
(le 1 se trouve sur l'axe des ordonnées, on "va jusqu'à la droite puis jusqu'à l'axe des abscisses" pour trouver 2)
2. Comme la courbe représentative de cette fonction est une droite qui passe par l'origine, il s'agit forcément d'une fonction linéaire. (ne pas oublier cette phrase !)
On sait donc que son expression est de la forme \(x \mapsto ax\).
Ensuite, on peut trouver sa pente de différentes façons:
Mieux vaut lire l'image de 2, de 4 ou de 6 qui sont beaucoup plus claires.
On trouve ensuite que dans l'expression \(x \mapsto ax\), le nombre \(a\) peut se calculer au choix par \(\frac{1}{2}\) , \(\frac{2}{4}\) ou \(\frac{3}{6}\)
puisqu'il faut que \(2 \mapsto a\times 2 = 1\) , \(4 \mapsto a\times 4 = 2\) et \(6 \mapsto a\times 6 = 3\).
Je vais m'intéresser aux deux derniers: (2;1) et (4;2)
L'écart horizontal entre les deux est de 2 et l'écart vertical est de 1, on obtient donc une pente de \(\frac{1}{2}\)
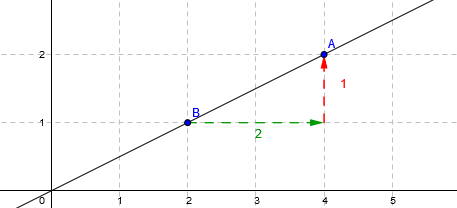
(bien sûr vous pouvez aussi écrire \(g:x\mapsto 0,5x\) !)
une fois de plus, si vous préférez écrire que \(g(9)=4,5\), pas de problème !
40 p127: trouver l'expression d'une fonction pour confirmer (ou non) une lecture graphique
(Vous avez remarqué que l'exercice parle de fonction affine et pas de fonction linéaire ?? Faisons comme si de rien n'était, j'en reparle tout à l'heure...)
1. On nous demande si le point M de coordonnées (2;0,8) appartient à la droite. Cela semble raisonnable mais difficile d'être sûr...
2. a. Les noeuds du quadrillage correspondent à ce que j'appellais plus haut "des points dont les coordonnées sont claires".
Sur cette droite il n'y en a pas beaucoup... Je vois uniquement (0;0) et (5;2).
b. Comme nous la droite passe par (0;0), c'est à dire l'origine du repère, elle représente une fonction linéaire (donc de la forme \(x \mapsto ax\).
Et comme de plus, la droite passe par (5;2), l'image de 5 est 2.
En résolvant \(a \times 5 = 2\) on trouve que \(a=\frac{2}{5}\) (on peut aussi le "voir" en obeservant la pente: on doit avancer de 5 cases pour monter de 2 cases).
On en conclue que \(f:x\mapsto \frac{2}{5}x\).
3. On peut maintenant vérifier par calcul notre lecture graphique du début, c'est à dire vérifier que l'image de 2 par \(f\) est (ou pas) 0,8:
\(f(2)= \frac{2}{5} \times 2 = \frac{4}{5}=0,8\)
Notre observation est bien confirmée par le calcul.
Retenez que l'obervation donne des idées "facilement" et rapidement mais l'exactitude ne peut souvent être obtenue que par calcul:
considérez les valeurs observées comme des valeurs approchées tant qu'elles n'ont pas été confirmées par un calcul exact !
Nous avions déjà remarqué qu'on peut passer de la 1ere à la 2eme ligne en multipliant par 3. Par contre il est moins facile de passer directement de la 1ere ligne à la 3eme et ces deux lignes ne sont pas proportionnelles (dans une relation de proportionnalité, l'image de 0 est toujours 0 ! Déjà...). Passer de la 2eme ligne à la 3ème n'est pas si dur... il suffit d'ajouter 2. Finalement, pour trouver l'image d'un nombre par \(g\), il faut donc multiplier par 3 puis ajouter 2. Voici les deux fonctions représentées dans un repère: Pour finir, regardez l'image de 0. Une fonction affine est une donction de la forme \(x \mapsto ax+b\) avec \(a\) et \(b\) des nombres relatifs quelconques. Sa représentation est une droite. On peut les voir comme des "fonctions linéaires décalées". On retrouvera la même notion de pente, qui correspondra au nombre \(a\) et le "décalage" sera la conséquence du nombre \(b\), on l'appelle l'ordonnée à l'origine. Regardez cette animation et jouez avec les curseurs: En jouant avec les curseurs, si vous mettez \(b\) à 0, vous vous retrouverez avec une fonction linéaire. Les fonctions linéaires SONT des fonctions affines particulières.
Cours
Observons le tableau ci-dessous:
Nous connaissons déjà la fonction \(f\), comment passer de l'image de \(x\) par \(f\) à son image par \(g\) ?
\(x\)
...
-3
-2
-1
0
1
2
3
...
\(f(x)\)
...
-9
-6
-3
0
3
6
9
...
\(g(x)\)
...
-7
-4
-1
2
5
8
11
...
La fonction \(f\) est \(x \mapsto 3x\) et les 2 premières lignes forment un tableau de proportionnalité.
On peut en conclure que \(g:x\mapsto 3x+2\).
(je vous avais déjà fait trouver une telle fonction lors du chapitre N9).
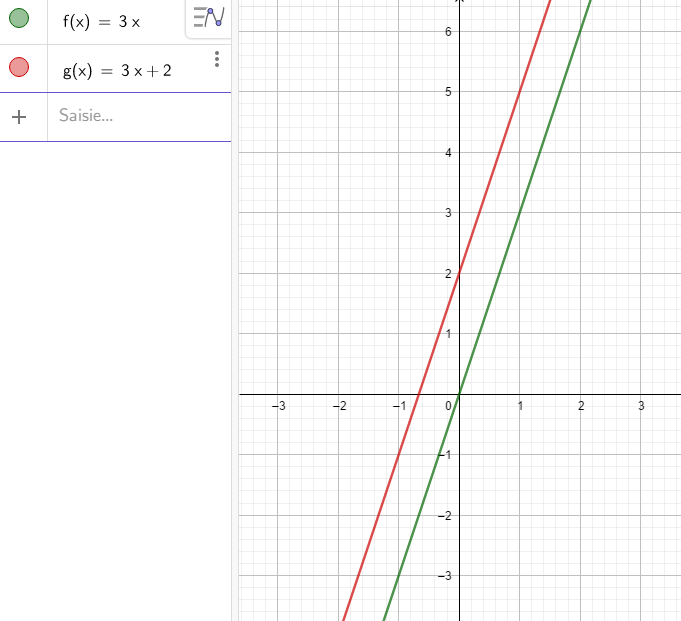
On remarque que la courbe rouge, correspondant à \(g:x\mapsto 3x+2\), est aussi une droite (mais elle ne passe pas par l'origine).
On peut remarquer aussi qu'elle est "décalée de 2 vers le haut" par rapport à la droite verte représentant \(f:x \mapsto 3x\). C'est logique puisqu'une image par \(g\) peut se trouver en ajoutant 2 à celle par \(f\).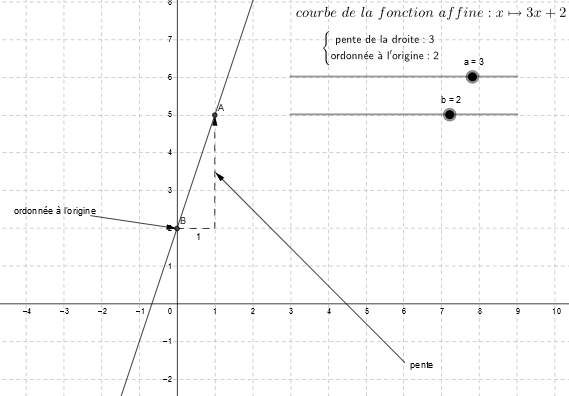
15 p124 reconnaitre si une fonction est affine par son expression 16 p123 représenter graphiquement une fonction affine 20 p124 trouver l'expression d'une fonction affine par lecture graphique (pente et ordonnée à l'origine) A faire



