
3èmes - jeudi 28 mai: fonctions affines
Résumé de la séance:
- reconnaitre une fonction affine (à partir de son expression ou de sa courbe représentative)
- trouver les paramètres d'une fonction affine (à partir de son expression ou de sa courbe représentative)
- tracer la droite représentative d'une fonction affine (à partir de son expression)
On reconnait l'expression d'une fonction affine si on peut trouver les nombres \(a\) et \(b\) pour que l'expression \(x\mapsto ax+b\) soit conforme à la fonction. a. \(f(x)=6x-3\) cette fonction est bien une fonction affine avec \(a=6\) et \(b=-3\). b. \(g(x)=-4x^2\) cette fonction n'est pas affine (à cause de la présence du \(x^2\)). c. \(h(x)=\frac{1}{x}+7\) cette fonction n'est pas affine. On ne peur pas trouver de nombre par lequel multiplier \(x\) pour correspondre à \(\frac{1}{x}\). d. \(k(x)=\frac{x}{2}-5\) en revanche, cette fonction est affine. \(a=\frac{1}{2}\) et \(b=-5\). Vous pouvez bien sûr construire un tableau de valeurs, comme pour n'importe quelle fonction avant de placer des points dans le repère. Mais comme les fonctions affines sont représentées par des droites, 2 points suffiront. En manipulant l'animation geogebra du dernier cours, vous avez pu vous rendre compte que des fonctions avec la même pente (le nombre \(a\)) sont parallèles. Pour obtenir la correction, vous pouvez utiliser mon animation geogebra en manipulant les curseurs ou tracer vous-même les fonctions dans geogebra: a. \(f(x)=3x-2\) Pour obtenir un premier point, l'idéal est de trouver l'ordonnée à l'origine: ici -2 (c'est le nombre \(b\)) → Donc la droite doit passer par le point (0;-2). Ensuite, pour trouver un deuxième point, on peut utiliser la pente (c'est le nombre \(a\)): ici 3 → En partant du premier point: on se décale d'1 case vers la droite puis de 3 cases vers le haut →dernière étape: tracer la droite passant par ces 2 points b. \(g(x)=-2x+4\) L'ordonnée à l'origine est 4 et la pente -2. c. \(h(x)=-x+1\) L'ordonnée à l'origine est 1 et la pente -1. d. \(k(x)=-3x\) L'ordonnée à l'origine est 0 et la pente -3. (il s'agit d'une fonction linéaire !) C'est le travail inverse. En observant des points stratégiques, on peut rapidement trouver les nombres \(a\) et \(b\). Repères: Toutes les fonctions représentées dans cet exercices sont des fonctions affines puisque toutes les courbes sont des droites. Elles auront donc toutes des expressions de la forme \(x \mapsto ax+b\). (Je ne le préciserai donc pas à chaque fois) 1. Finalement: \(f:x\mapsto -2x+1\). 2. Finalement: \(g:x\mapsto \frac{1}{2}x\). 3. Finalement: \(h:x\mapsto x+3\). 4. Finalement: \(k:x\mapsto \frac{-5}{2}x+5\). → n'hésitez jamais à vérifier que vos expressions sont cohérentes avec les points de la droite dont les coordonnées sont "faciles" à lire ex: \(f:1\mapsto -2 \times 1+1 =-1\) ça marche (le point (1;-1) appartient bien à \((d_1)\)) \(k:2\mapsto \frac{-5}{2}\times 2+5 =-5+5 = 0\) ça marche (le point (2;0) appartient bien à \((d_4)\))
Correction
15 p124: reconnaitre si une fonction est affine par son expression
16 p123: représenter graphiquement une fonction affine
Le nombre \(b\) donne le "décalage" de la fonction affine \(x\mapsto ax+b\) par rapport à la fonction linéaire \(x\mapsto ax\).
Ce "décalage" s'appelle l'ordonnée à l'origine de la droite. Ce nom vient du fait qu'il correspond à l'image de 0. (c'est l'ordonnée du point où la droite coupe l'axe des ordonnées)
En effet, peut importe la valeur de \(a\) quand \(x=0\), on obtient: \(0 \mapsto a\times0+b=b\).
L'animation est justement faite pour indiquer l'effet des paramètres \(a\) et \(b\) sur la droite à tracer.
Téléchargez l'application (geogebra classique 5) ou utilisez la en ligne.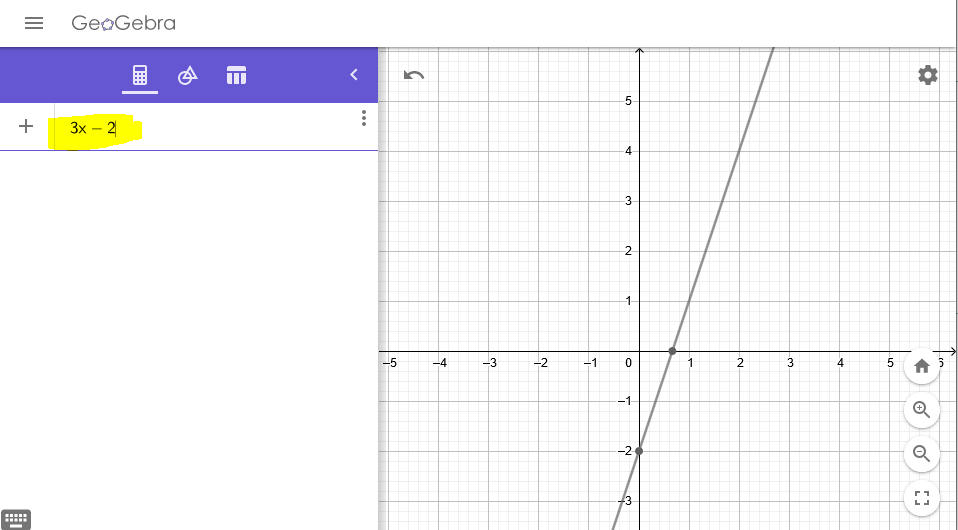
On obtient le point (1;1).
→ Premier point: (0;4)
→ En partant de ce point: on se décale d'1 case vers la droite puis de 2 cases vers le bas pour arriver en (1;2)
→ On trace la droite passant par ces deux points
→ Premier point: (0;1)
→ En partant de ce point: on se décale d'1 case vers la droite puis de 1 case vers le bas pour arriver en (1;0)
→ On trace la droite passant par ces deux points
→ Premier point: (0;0)
→ En partant de ce point: on se décale d'1 case vers la droite puis de 3 cases vers le bas pour arriver en (1;-3)
→ On trace la droite passant par ces deux points 20 p124: trouver l'expression d'une fonction affine par lecture graphique (pente et ordonnée à l'origine)
Sinon, il reste la possibilité de dresser un tableau de valeurs et d'essayer de trouver la multiplication et l'addition à faire...
→ on en déduit que \(a=\frac{-2}{1}=-2\).
→ on en déduit que \(a=\frac{1}{2}\).
→ on en déduit que \(a=\frac{1}{1}=1\).
→ on en déduit que \(a=\frac{-5}{2}\).
On continue l'entrainement:
21 p125 reconnaitre si une fonction est affine ou linéaire en observant sa courbe 22 p123 identifier les paramètres d'une fonction affine à partir de son expression 23 p124 identifier les paramètres d'une fonction affine par lecture graphique (pente et ordonnée à l'origine) 24 p125 trouver un point à partir d'indices (vous aller devoir tracer les droites !) A faire
→ "coefficient directeur" = "pente"



