journal des 3èmes: semaine du 26 au 30 avril 2021 (séance 2/3)
Résumé de la séance:
- statistiques: notions de moyenne, médiane et étendue
méthode pour la moyenne:
- on calcule la somme des valeurs de la série
- puis on divise cette somme par l'effectif total de la série
→ on obtient la valeur qui donnerait le même total si toutes les données avaient eu la même valeur, c'est la moyenne
méthode pour la médiane:
- il faut commencer par classer les données dans l'ordre croissant
- ensuite, il faut déterminer la position de la médiane (en coupant l'effectif en 2 parts égales)
- enfin, trouver la "valeur du milieu" ou calculer la moyenne des "2 valeurs du milieu"
→ on obtient une valeur qui permet de dire qu'au moins la moitié des valeurs lui sont inférieurs ou égales (et aussi la moitié des valeurs lui sont supérieures ou égales), c'est la médiane
méthode pour l'étendue:
- on trouve la valeur minimale et la valeur maximale de la série
- on caulcule l'écart entre les 2 (soustraction), on obtient l'étendue
a. Pour la suite, il faut classer les données dans l'ordre croissant: calcul de la médiane: calcul de l'étendue: \(valeur~maximale - valeur~minimale = 20-6 = 14\) b. Données classées dans l'ordre croissant: calcul de la médiane: calcul de l'étendue: \(valeur~maximale - valeur~minimale = 12-2 = 10\) c. calcul de la moyenne: \( \frac{3+5+3+7+2+2+8+4}{8}=\frac{34}{6}=4,25\) Données classées dans l'ordre croissant: calcul de la médiane: calcul de l'étendue: \(valeur~maximale - valeur~minimale = 8-2 = 6\) Données classées dans l'ordre croissant: 1. La plus grande valeur est 41m et la plus petite 32m. 2. L'étendue est donc de 9m (41m - 32m). 3. La hauteur moyenne est 36m (180m au total, divisé par 5). 4. La médiane est 35m (la 3ème valeur dans l'ordre croissant). 1. Au total, il y a donc \(2+6+3+1+3=15\) enfants. 2. Pour l'âge moyen, il faut prendre en compte qu'ils sont 2 à avoir 13ans, 6 à avoir 14ans, etc... quand on calcule le total ! 222 ans au total pour 15 enfants donne une moyenne de \(\frac{222\,ans}{15}=14,8\,ans\). 3. Comme il y a 15 enfants, la médiane est l'âge du 8ème enfant (\(15 = 7+1+7\)). Avec un tableur, cela peut se faire avec ces formules: En regardant le tableau avec les effectifs, on s’aperçoit que le 8ème enfant a 14 ans. 2. Le jour le moins pluvieux est le vendredi avec 0 mm de pluie. 3. La remarque de Léa correspond à la notion de moyenne. S'il avait plu 9 mm tous les jours, cela aurait fait un total de \(7\times 9\,mm = 63\,mm\) de pluie sur la semaine. Correction:
1p162
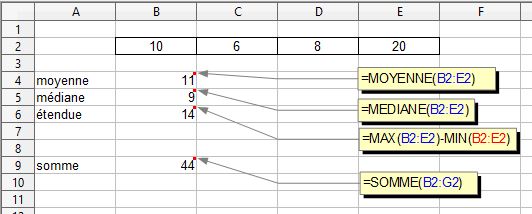
calcul de la moyenne: \( \frac{somme~des~valeurs}{nombre~de~valeurs}=\frac{10+6+8+20}{4}=\frac{44}{4}=11\)
(avec une série de 4 valeurs toutes égales à 11, on obtiendrait bien un total de 44)
numéro de la donnée
1ere
2eme
3eme
4eme
valeur de la donnée
6
8
10
20
Il y a 4 valeurs (c'est un nombre pair, il n'y a donc pas de valeur du milieu, il va falloir en "inventer" une). On calcule la moyenne entre les 2 valeurs du milieu (la 2ème et la 3ème):
\( \frac{8+10}{2}=\frac{18}{2}=9 \)
(la moitié des valeurs de la série sont inférieures à 9 et l'autre moitié sont supérieures à 9)
(il y a 14 d'écart entre la plus grande valeur de la série et la plus petite)
calcul de la moyenne: \( \frac{2+12+4+6+8+12}{6}=\frac{44}{6}\approx 7,33\)
numéro de la donnée
1ere
2eme
3eme
4eme
5eme
6eme
valeur de la donnée
2
4
6
8
12
12
Il y a 6 valeurs. On calcule la moyenne entre les 2 valeurs du milieu (la 3ème et la 4ème):
\( \frac{6+8}{2}=\frac{14}{2}=7 \)
numéro de la donnée
1ere
2eme
3eme
4eme
5eme
6eme
7eme
8eme
valeur de la donnée
2
2
3
3
4
5
7
8
Il y a 8 valeurs. On calcule la moyenne entre les 2 valeurs du milieu (la 4ème et la 5ème):
\( \frac{3+4}{2}=\frac{7}{2}=3,5 \) 2p162 hauteurs de peupliers
numéro de la donnée
1ere
2eme
3eme
4eme
5eme
valeur de la donnée
32m
34m
35m
38m
41m
13 p164 âges des enfants d'un camp de vacances
Il y a 2 enfants de 13ans, 6 de 14ans, etc...
\( 2\times13+6\times14+3\times15+1\times16+3\times17 = 26+84+45+16+51=222\)
Dans la dernière colonne de cette ligne, on retrouve l'effectif total, en effet "il y a 15 enfants de 17 ans ou moins".
L'age médian de ce camp de vacances est donc 14 ans. 10 p164 pluviomètre
Par exemple, on voit que le lundi, il a plu 10 mm.
Or il a plu \(10\,mm+14\,mm+8\,mm+16\,mm+0\,mm+4\,mm+6\,mm= 58\,mm\).
Elle a donc tort. La moyenne de précipitation de cette semaine est en fait \(\frac{58\,mm}{7}\approx 8,3\,mm\).
7 p163 temps de course (vu au brevet) 8 p163 salaires dans une entreprise 9 p163 ventes de la journée pour une boutique (faites le directement au tableur si possible) 15 p164 enquête sur le nombre de spams reçus en un week-end A faire: