
journal des 4èmes: jeudi 29 avril 2021
Résumé de la séance:
- utiliser les propriétés sur les angles alternes-internes et les angles opposés par le sommet (faire une démonstration)
L'objectif des exercices à faire pour aujourd'hui est d'utiliser les 3 propriétés suivantes: Propriété 1: Si deux angles sont opposés par le sommet alors ils sont de même mesure. Propriété 2: Si deux angles alternes-internes sont formés par deux droites parallèles coupées par une (3ème droite) sécante alors ils sont de même mesure. Propriété 3: Si deux angles alternes-internes sont formés par deux droites coupées par une (3ème droite) sécante et qu'ils sont de même mesure alors les deux (premières) droites sont parallèles. → la propriété 2 implique que: si les angles alternes-internes ne sont pas de même mesure alors les deux droites ne peuvent pas être parallèles → la propriété 3 implique que: si les deux droites ne sont pas parallèles alors les angles alternes-internes ne peuvent pas être de même mesure Une propriété (ou théorème), s'utilise dans une sens. La plupart du temps c'est une phrase avec "SI ... ALORS ...". Les deux parties remplaçant les "..." s'appellent "hypothèses" et "conclusion". Les hypothèses sont des conditions à vérifier avant d'utiliser une propriété. Si ces conditions sont vérifiées, on peut utiliser la propriété pour en tirer une nouvelle certitude: sa "conclusion". Les propriétés 2 et 3 sont les réciproques l'une de l'autre. On peut les schématiser par: En revanche, la réciproque de P1 n'est pas vraie. Cette propriété ne s'utilise que dans un sens: mais la phrase suivante est FAUSSE: "Si deux angles sont de même mesure alors ils sont opposés par le sommet." Cours
P2: droites parallèles → angles alternes-internes de même mesure
P3: angles alternes-internes de même mesure → parallèles
P1: opposés par le sommet → même mesure
(la réciproque de P1 est fausse)
Seuls es angles de la figure b sont alternes-internes. Les angles de la figure a sont dit "correspondants" (avec des propriétés similaires à P2 et P3 mais ce n'est plus au programme). Les angles des figures c et d n'ont rien à voir. Les angles colorés sont alternes-internes. a. Sur la figure, on peut comprendre immédiatement que les angles sont de même mesure mais avec les propriétés à notre disposition il va falloir le démontrer en 2 étapes. L'idéal serait de donner des noms aux 3 angles de la figure ci-dessus mais je vais uniquement utiliser les couleurs. Les angles vert et rouge sont alternes-internes. Comme \((d_1)\) et \((d_2)\) sont parallèles, ces angles sont de même mesure. Les angles vert et violet sont opposés par le sommet. Ils sont donc de même mesure. Finalement, les 3 angles marqués sont de même mesure (34°). Je sais bien qu'il est tentant de dire "ça se voit que les droites ne sont pas parallèles" mais rappelez vous qu'il faut se méfier d'un schéma et n'utiliser que les informations fiables (c'est à dire celles données par l'énoncé ou le codage). Là aussi il va falloir procéder en plusieurs étapes.
Correction
2 p220 reconnaitre des angles alternes-internes
5p220 rédiger une démonstration en utilisant une propriété
Donc si les droites \((d_1)\) et \((d_2)\) sont parallèles, on peut en conclure que ces angles sont égaux.
6 p220 rédiger une démonstration en utilisant une propriété
(ce qui n'était pas le cas quand on voyait les angles correspondants...)
7 p220 rédiger une démonstration
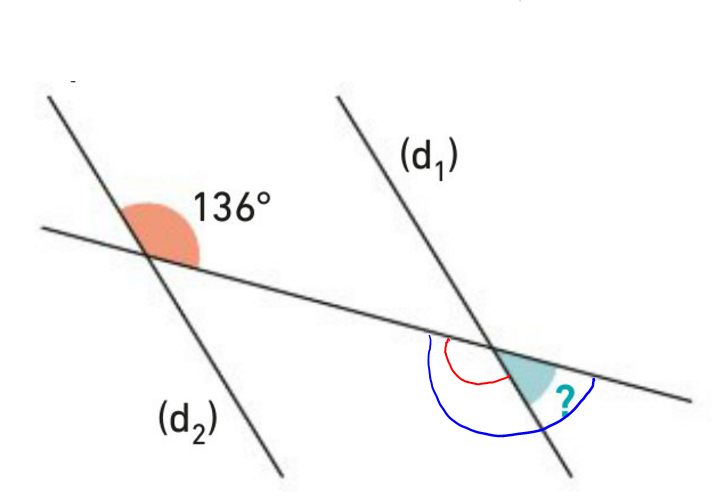
Donc la mesure de l'angle rouge est 136°.
On peut en conclure que l'angle vert mesure 44° (180°-136°).
On continue sur le même thème:
A faire
8 p220 à partir d'une seule mesure d'angle on peut trouver les mesures de TOUS les autres angles de la figure
9 p220 expliquer des parallèles
11 p220 trouver tous les angles de la figure (sans démonstration)
12 p220 exploitez l'angle droit du codage et vos connaissances sur les angles alternes-internes



