
3èmes - Lundi 18 mai ~ vendredi 22 mai (1/2): fonctions linéaires
Résumé de la séance:
- exercices de proportionnalité divers
- découverte de fonctions particulières: les fonctions linéaires
(avec la flèche portant un "\(\times 3\)" pour passer de la 1ère à la 2ème ligne) Il s'agit d'un tableau de porportionnalité puisqu'une multiplication (toujours par le même nombre) permet de passer d'une ligne à l'autre. 2) La fonction correspondante est \(x \mapsto 3x\). C'est la fonction qui renvoie le triple d'un nombre. 3) Cette fonction est linéaire, elle est bien de la forme \(x \mapsto ax\) avec \(a=3\) (bref, c'est une fonction qui ne fait que multiplier le nombre de départ). 4) a. \(g(x)=7x\) est la fonction qui correspond au programme de calcul "Je multiplie \(x\) par 7". b. \(h(x)=-3x\) est la fonction qui correspond au programme de calcul "Je multiplie \(x\) par -3". c. \(k(x)=\frac{1}{2}x\) est la fonction qui correspond au programme de calcul "Je multiplie \(x\) par \(\frac{1}{2}\)". 5) Avec les tableaux de valeurs fournis par l'exercice on trouve: a. \(m(x)=2x\) (qu'on peut aussi écrire \(m:x\mapsto 2x\)). b. \(n(x)=-3x\) (qu'on peut aussi écrire \(n:x\mapsto -3x\)). c. \(p(x)=-5x\) (qu'on peut aussi écrire \(p:x\mapsto -5x\)). \(f\) est la fonction définie par \(f(x)=3x\). 1) coordonnées du point de la courbe de \(f\) correspondant La deuxième ligne s'obtient en multipliant la première par 3. 2) a. b. Ces points font partie de la courbe de la fonction \(f\). Comme on se rend compte que tous les points que nous avons placés sont alignés, on peut imaginer que la courbe complète est une droite. Bref, voici la courbe de \(f\): Remarque: en mathématique une courbe peut être droite !!! (Ce qui n'est pas vraiment le cas dans le langage courant) 3) La courbe bleue correspond à la fonction \(f\) du début de l'exercice (la fonction qui multiplie par 3) La courbe rouge correspond à \(g\) (la fonction qui multiplie par 2) La courbe verte correspond à \(h\) (la fonction qui multiplie par -2) Correction
activité 1 p118: trouver une fonction linéaire à partir d'un tableau de valeurs
1)
-2
0
2
4
-6
0
6
12
activité 2 p118: tracer la courbe d'une fonction linéaire
\(x\)
-2
-1
0
1
3
5
\(f(x)\)
-6
-3
0
3
9
15
(-2;-6)
(-1;-3)
(0;0)
(1;3)
(3;9)
(5;15)
En général, on n'écrit jamais la troisième ligne. C'est uniquement parce que c'est une activité de découverte qu'on vous le demande ici.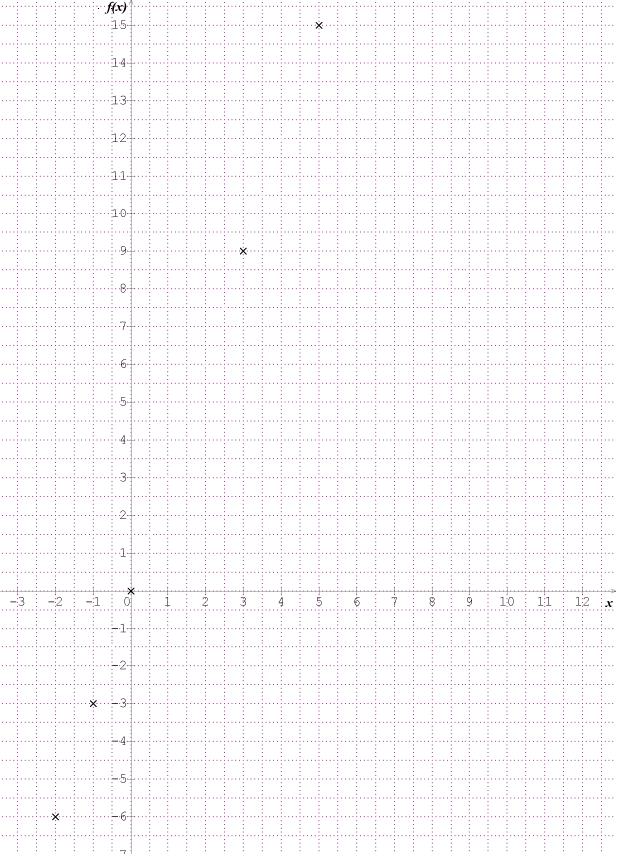
(pour obtenir tous les points de la courbe, il faudrait théoriquement faire un tableau de valeurs avec tous les nombres de départ possibles, et toutes leurs images !)
On peut même faire plus que le supposer si:
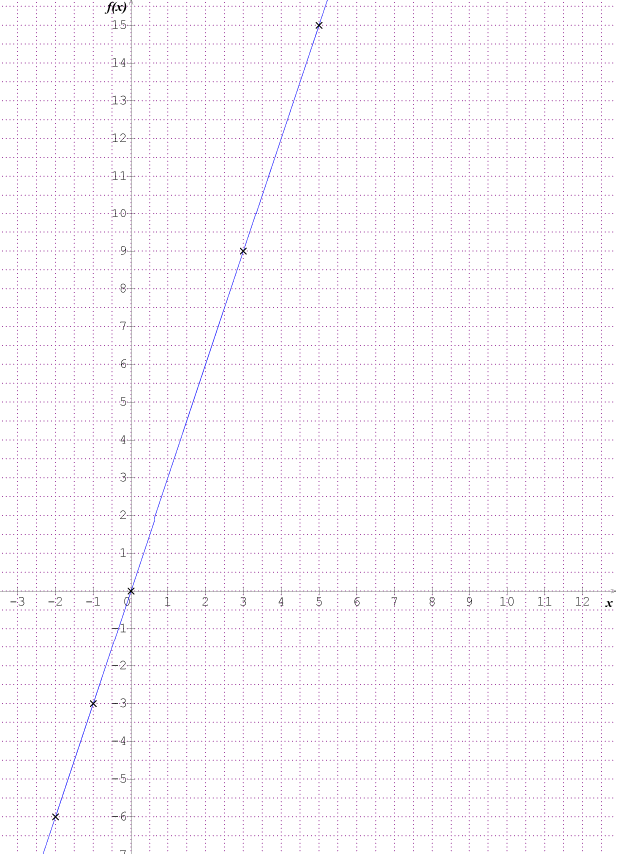
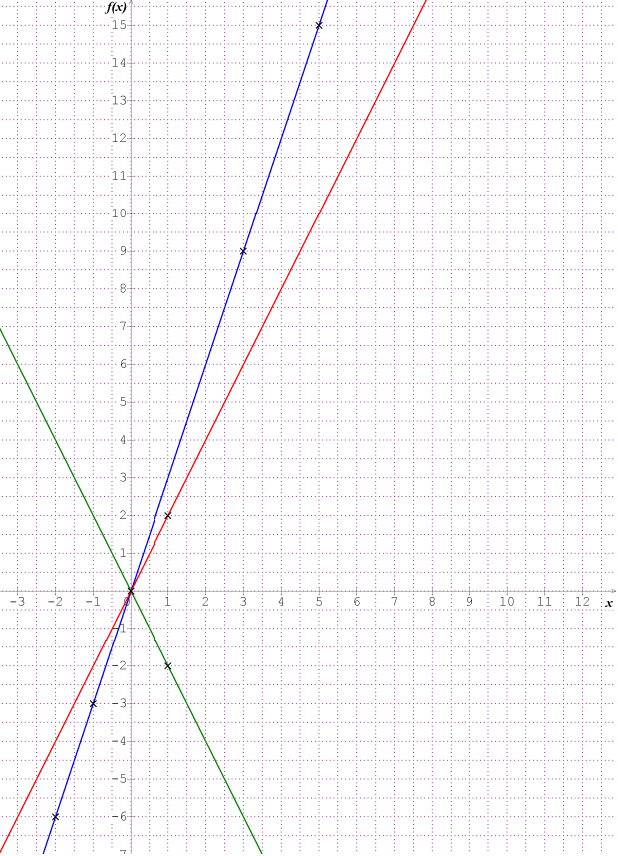
→ on l'a obtenu avec 6 points mais quand on sait qu'on doit trouver une droite, 2 points suffisent !
→ on sait que la droite à trouver doit passer par l'origine du repère (le point de coordonnées (0;0)). Il suffit donc de trouver un deuxième point.
L'idéal, souvent, est de trouver l'image de 1: \(g(1)=2 \times 1 = 2\)
Donc la droite rouge doit passer par \((1;2)\).
→ la droite verte doit passer par \((1;-2)\)
Pour trouver la droite représentant une fonction linéaire \(f: x \mapsto ax\), il suffit de tracer la droite passant par \((0;0)\) et un point de coordonnées \((x;ax)\). On prend souvent le point \((1;a)\) (surtout si \(a\) est un nombre entier) A retenir
3 p122 reconnaître si une fonction est linéaire à partir de son expression 4 p122 reconnaître si une fonction est linéaire à partir de sa représentation graphique 6 p122 tracer la représentation graphique d'une fonction linéaire à partir de son expression A faire
(la fonction revient elle simplement à multiplier le nombre de départ ? Par combien ?)
(bien faire les 4 exemples)
(chercher d'abord l'image du nombre 1 ou d'un autre qui vous arrange mieux...)



