3èmes - vendredi 29 mai: fonctions affines
Résumé de la séance:
- reconnaitre une fonction affine (à partir de son expression ou de sa courbe représentative)
- trouver les paramètres d'une fonction affine (à partir de son expression ou de sa courbe représentative)
- tracer la droite représentative d'une fonction affine (à partir de son expression)
- application concrète
Correction
21 p125 reconnaitre si une fonction est affine ou linéaire en observant sa courbe
- \(\cal (C_1)\) est la courbe d'une fonction affine (puisque c'est une droite)
- \(\cal (C_2)\) est la courbe d'une fonction affine (puisque c'est une droite)
et plus précisément,
\(\cal (C_2)\) est la courbe d'une fonction linéaire (puisque cette droite passe par l'origine)→ les fonctions linéaires font partie des fonctions affines
- \(\cal (C_3)\) n'est pas la courbe d'une fonction affine (puisque ce n'est pas une droite)
pour aller plus loin (hors programme, sera vu en seconde):
vous pouvez reconnaitre une parabole (on en avait déjà parlé, rapidement...)
c'est caractéristique d'une fonction avec des \(x^2\) dans son expression
cela correspond à la trajectoire d'un objet jeté - \(\cal (C_4)\) est la courbe d'une fonction affine (puisque c'est une droite)
plus particulièrement:
- il s'agit d'une fonction constante (qui renvoie toujours la même valeur)
- la pente de cette droite est nulle (=0)
22 p123 identifier les paramètres d'une fonction affine à partir de son expression
→ Comme je l'avais indiqué: "coefficient directeur" et "pente" signifient la même chose
| fonction | pente | ordonnée à l'ortigine | |
| a. | \(f(x)=4x+5\) | 4 | 5 |
| b. | \(g(x)=-2x-5\) | -2 | -5 |
| c. | \(h(x)=6\) | 0 | 6 |
| d. | \(k(x)=7-5x = -5x+7\) | -5 | 7 |
Petit piège de la part du livre dans la question d... Vous êtes tombés dedans ??
23 p124 identifier les paramètres d'une fonction affine par lecture graphique
| droite | coefficient directeur | ordonnée à l'origine | fonction représentée |
| (\(d_1)\) | 2 | 1 | \(x \mapsto 2x+1\) |
| (\(d_2)\) | -3 | 3 | \(x \mapsto -3x+3\) |
| (\(d_3)\) | \(\frac{2}{4}=\frac{1}{2}\) | -1 | \(x \mapsto \frac{1}{2}x-1\) |
| (\(d_4)\) | \(\frac{-1}{2}\) | 4 | \(x \mapsto \frac{-1}{2}x+4\) |
24 p125 trouver un point à partir d'indices (en traçant des droites !)
Le seul point avec des coordonnées entières dans la zone indiquée est (2;4).
Cours
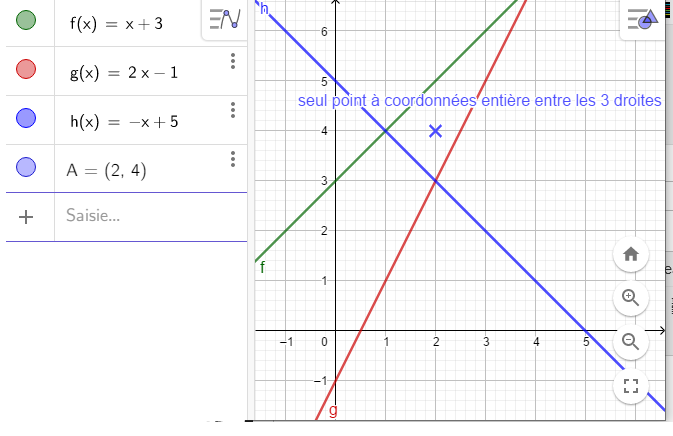
Jusque là, les paramètre des fonctions affines étaient "relativement faciles" à trouver (en particulier, l'ordonnée à l'origine était toujours un nombre entier).
Voici une méthode générale pour trouver les paramètres d'une fonction affine lorsqu'on connait les coordonnées de 2 points de sa droite:
- Première étape: trouver la pente
→ calcul du rapport "déplacement vertical / déplacement horizontal" - Deuxième étape: trouver l'ordonnée à l'origine
→ résolution d'une (petite) équation
C'est ce qui est détaillé dans l'animation suivante:
Le calcul de la pente (j'espère qu'il est assez clair...) correspond à la formule (qui me parait compliquée) du paragraphe 3 p121 du livre.
Faites variez les curseurs et voyez le changement des calculs.
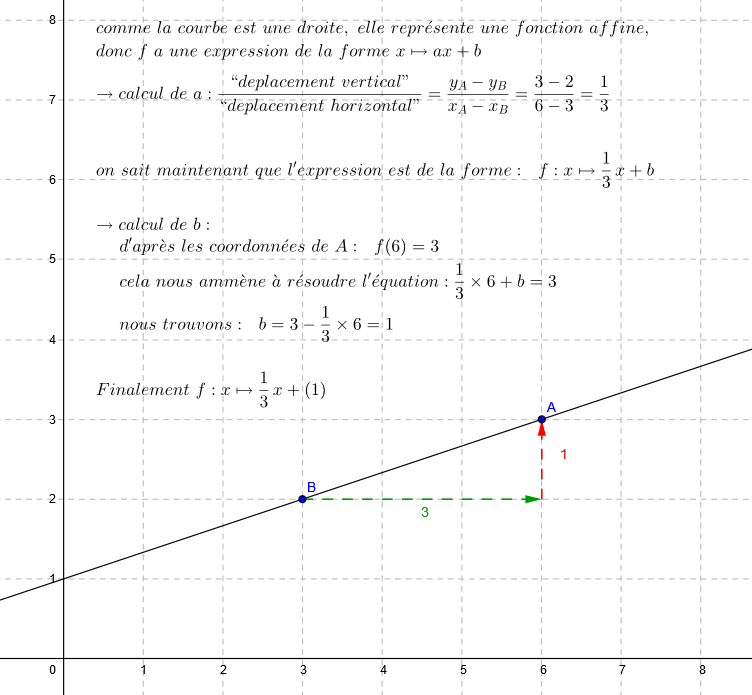
Essayons d'appliquer tout ce qu'on a vu sur les fonctions affines (sur du concret):
A faire
avec ce qu'on a vu avant aujourd'hui:
27 p125 prix du téléphone avec hors-forfait
→ appelez \(x\) le nombre de minutes appelées dans le mois
avec ce qu'on a vu aujourd'hui:
29 p126 (pas très concret mais permet d'appliquer le cours d'aujourd'hui)
→ ne pas hésiter à placer les points dans un repère et tracer la droite pour y voir plus clair
37 p126 (pas très concret mais plus simple: il suffit de vérifier si les valeurs "collent")
43 p127 Joe le taxi