3emes N6 Equation: exercice - correction complète
Figure:
Correction:
a) Écrire en fonction de \(x\) le périmètre \(p_1(x)\) de TROP.
Le périmètre de TROP peut s'écrire:
\(2+x+2+x\) (on additionne chaque côté) ou encore \(2 \times 2+ 2 \times x \) (2 longueurs + 2 largeurs) ou encore \(2x+4\) (expression réduite égale aux 2 autres).
\(p_1(x)=2x+4\)
b) Écrire en fonction de \(x\) le périmètre \(p_2(x)\) de CHER.
Pour le périmètre de CHER, il faut faire attention au fait que sa longueur vaut \((6-x)\) !
Le périmètre de CHER peut s'écrire:
\(1+6-x+1+6-x\) (on additionne chaque côté) ou encore \(2 \times 1+ 2 \times (6-x) \) (2 longueurs + 2 largeurs) ou encore \(-2x+14\) (expression réduite égale aux 2 autres).
\(p_2(x)=-2x+14\)
c) Représenter graphiquement dans un même repère les fonctions \(p_1\) et \(p_2\).
Pour commencer, il est judicieux de s'interroger sur l'étendue des valeurs possibles pour \(x\):
Ses valeurs vont de 0 minimum à 6 maximum dans cet exercice.
Pour \(x=2\), on obtient un périmètre de TROP de: \(p_1(2)=2\times2+4=8\) et un périmètre de CHER de: \(p_2(2)=-2\times2+14=10\)
Pour \(x=5\), on obtient un périmètre de TROP de: \(p_1(5)=2\times5+4=14\) et un périmètre de CHER de: \(p_2(5)=-2\times5+14=4\)
etc ...
En complétant avec d'autres calculs, on obtient un tableau de valeurs pour \(p_1\) et \(p_2\):
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(p_1(x)\) | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| \(p_2(x)\) | 14 | 12 | 10 | 8 | 6 | 4 | 2 |
On pourrait faire de nombresuses remarques sur ce tableau et les courbes qui vont suivre car ces fonctions sont particulières (nous les étudieront dans un prochain chapitre: les fonctions affines...).
Enfin, placez des points dans un repère (bien choisir la taille des axes et les unités à partir des valeurs minimales et maximales obtenues dans les tableaux !).
C'est une bonne idée d'utiliser des points de couleurs différentes (une couleur par fonction/rectangle).
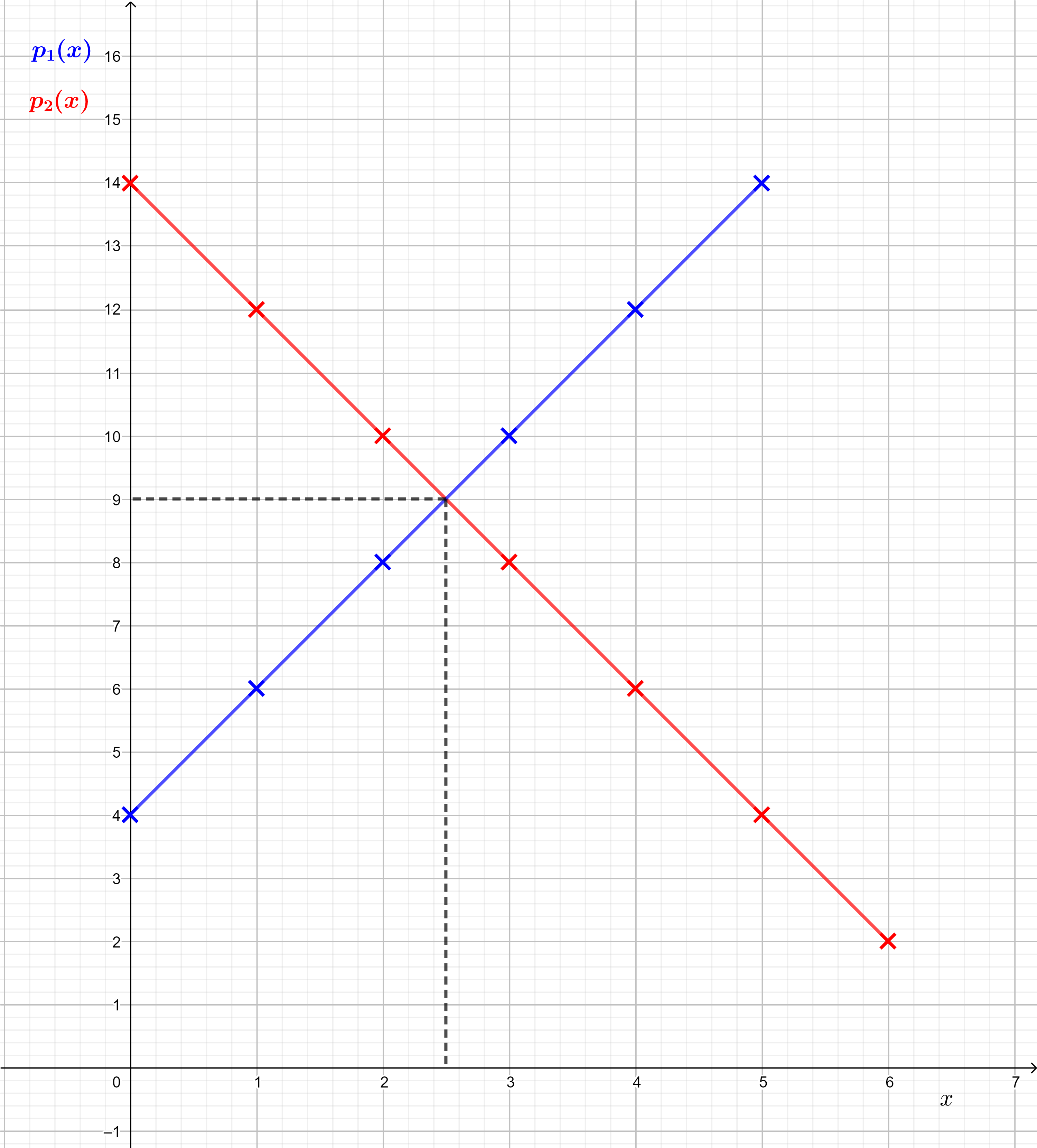
Avec les données du tableau, cela donne un graphique comme celui-ci:
On observe clairement que les points bleus, qui correspondent aux données pour \(p_1\), indiquent que sa valeur augmente en même temps que \(x\) et qu'inversement, les points rouges qui correspondent aux données pour \(p_2\), indiquent que sa valeur diminue quand \(x\) augmente.
Les points bleus sont alignés et les points rouges aussi. Il est donc assez naturel de tracer une droite bleue et une droite rouge (mais cela consiste à faire la supposition que les périmètres évoluent régulièrement entre les données que nous avons calculées).
Lire sur le graphique la valeur de \(x\) pour laquelle les deux périmètres sont égaux.
Grâce aux droites tracées, on observe un point d'intersection qui indique que pour une valuer de \(x\) comprise entre 2 et 3, les périmètres sont égaux. Je vous laisse lire le graphique ci-dessous pour estimer cette valeur plus précisément:
Retrouver ce résultat par calcul.
Il s'agit de résoudre ce problème: pour quelle valeur de \(x\) a-t-on \(périmetre_1 = périmètre_2\) ?
Autrement dit, résoudre:
\( p_1(x)= p_2(x)\)
ce qui revient à \( 2x+4 = -2x +14 \)
Après résolution, on trouve que \(x=\frac{5}{2}=2,5\). Et pour cette valeur de \(<\) on calcule \(p_2(2,5)=p_2(2,5)=9\).
C'est bien ce qu'on pouvait observer sur le graphique: le point d'intersection des deux courbes a pour coordonnées (2,5;9).
C'est donc pour TR=2,5cm qu'on obtient des périmètres égaux à 9 cm pour les deux rectangles.
d) Écrire en fonction de \(x\) l'aire \(\mathscr{A}_1(x)\) de TROP.
L'aire \(\mathscr{A}_1(x)=2x\) (aire d'un rectangle = longueur \(\times\) largeur).
e) Écrire en fonction de \(x\), l'aire \(\mathscr{A}_2(x)\) de CHER.
L'aire \(\mathscr{A}_2(x)=1\times (6-x)= -x+6\).
f) Pour quelle valeur de \(x\), les deux aires \(\mathscr{A}_1\) et \(\mathscr{A}_2\) sont-elles égales ?
On peut refaire un graphique:
Ou résoudre l'équation: \(\mathscr{A}_1(x)=\mathscr{A}_2(x)\)
Les deux méthodes permettent de trouver que \(\mathscr{A}_1(2)=\mathscr{A}_2(2)=4\).
C'est donc pour TR=2cm qu'on obtient des aires égales à 4 cm² pour les deux rectangles.