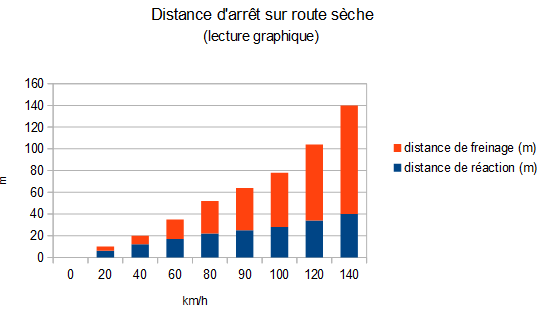
1)

a. D'après le premier graphique, la distance de réaction à 90 km/h est d'environ 25 m (ce serait présomptueux de donner une valeur exacte...).
A 90 km/h, le véhicule parcourt 25 m avant même que le conducteur ne touche la pédale de frein !

b. La distance de réaction est proportionnelle à la vitesse du véhicule puisque leur relation est représentée par une droite passant par l'origine.

2)

a. D'après le deuxième graphique, la distance de freinage sur route sèche à 90 km/h est de presque 40 m (encore une fois, difficile d'être précis).

b. La distance de freinage n'est pas proportionnelle à la vitesse puisque leur relation n'est pas représentée par une droite.

3)

a. La distance d'arrêt est la somme de la distance de réaction et de la distance de freinage:
à 90 km/h, le véhicule met:  \(25\,m + 40\,m=75\,m\) pour s'arrêter
→ le conducteur voit le danger, le véhicule parcourt 25m le temps qu'il commence à freiner, le conducteur appuie sur le frein et la voiture parcourt encore 40m avant de s'arrêter.
Au total, 75 m sont parcourus entre la vision du danger et l'arrêt total (à 90km/h).

b. En cumulant les distance de réaction et de freinage on obtient à peu près ce tableau pour la distance d'arrêt en fonction de la vitesse (sur route sèche, c'est pire sur route mouillée):

Avec le premier tableau j'obtiens ce graphique:

1.

a. On verra l'éclair avant d'entendre le tonnerre car la lumière est (beaucoup) plus rapide que le son.

En mettant ces deux vitesses dans les mêmes unités:

• vitesse du son = 340 m/s = 0,340 km/s   ce qui est déjà très rapide !
• vitesse de la lumière = 300 000 000 m/s = 300 000 km/s    avec les connaissances actuelles en physique, on pense que rien ne peut aller plus vite

b. La lumière va tellement vite que sur Terre qu'on voit un évènement presque instantanément. Pour un évènement se produisant à 12 km, la lumière met \(4\times 10^{-5}\,s\) (je suis obligé d'utiliser l'écriture scientifique tellement ce nombre est petit !).

Calcul: \(12\,km \div 300\,000\,km/s = 0,000 \,04\,s = 4 \times 10^{-5}\,s\)

c. Les 12 km sont parcourus par le son en environ 35 secondes.

Calcul: \(12\,km \div 0,340 \,km/s \approx 35,29\,s\)   (ou \(12\,000\,m \div 340 \,m/s \approx 35,29\,s\))

2.

a. 1 km est parcouru par le son en presque 3 secondes.

Calcul: \(1\,km \div 0,340 \,km/s \approx 2,94\,s\)   ou \(1\,000\,m \div 340 \,m/s \approx 2,94\,s\)

b. D'après la question précédente, on peut compter le nombre de secondes entre la vision de la foudre et le moment où on commence à entendre le tonnerre. Il suffit alors de diviser ce nombre de secondes par 3 pour obtenir à peu près le nombre de kilomètres.

Le plus simple pour résoudre cet exercice est de prendre un exemple:
Le taux obtenu sur cet exemple sera le même quelque soit le prix choisi puisque les proportions seront conservées.

Pour simplifier les calculs, prenons un prix rond de 100€ de prix de revient pour la chemise (c'est bien évidemment très exagéré !!!).
Dans ce cas, le coût de la main d’œuvre sera de 60€ et le coût des matériaux de 40€ (tissus et boutons).

Si le coût de la main d'oeuvre augmente de 10%, il passe à 66€    (10% de 60€ = 6€)
Si le coût des matériaux augmente de 30%, il passe à 52€    (30% de 40€ = 12€)

Le prix de revient passe alors à 118€  (66€+52€) et on comprend que l'augmentation du prix de revient est de 18%  (18€ sur les 100€ de départ).

Sans faire d'exemple:

• pour la main d'oeuvre, l'augmentation du prix de revient est de 10% de 60% soit de 6%
• pour les matériaux, l'augmentation du prix de revient est de 30% de 40% soit de 12%