6èmes - Jeudi 14 mai: proportionnalité
Résumé de la séance:
- vérifier si une situation est une situation de proportionnalité
Plusieurs méthodes pour savoir si les deux lignes de ce tableau sont proportionnelles: Dans notre tableau: On voit clairement que le rapport change (à part entre les deux premières colonnes). → Pour passer de 3 à 5, on peut multiplier par 0,6 (ou par \(\frac{3}{5}\) pour les experts des fractions que vous êtes !) → pour passer de 6 à 10, on peut multiplier par 0,6 aussi (\(\frac{6}{10}=\frac{3}{5}\)) → mais ensuite, il faut multiplier par 0,666... pour passer de 7 à 12, par 0,75 pour passer de 12 à 16, etc... Bref, très clairement, il n'existe pas de nombre qui marche à tous les coup pour passer de la première ligne à la deuxième ligne avec une simple multiplication. Les grandeurs du tableau ne sont donc pas proportionnelles. J'ai été très long (si vous avez tout déplié et tout lu...) pour vous expliquer les différentes possibilités mais quand vous avez trouvé où ça cloche, il suffit de le dire. La correction pourrait donc se résumer à: \(3 \times ... = 5\) → \(\frac{5}{3}\) \(18 \times ... = 20\) → \(\frac{20}{18}\) mais \(\frac{5}{3}=\frac{30}{18}~\neq \frac{20}{18} \) Donc, il ne faut pas multiplier par le même nombre pour passer de 3 à 5 et de 18 à 20. Les deux lignes du tableau ne sont pas proportionnelles. (et il y avait encore plus simple mais je m'arrête là pour cet exercice) 1) Peut on dire que Léa mesurera 2,80 m à 20 ans ?? Qui a dit oui ?! 2) Peut on prévoir la taille que Laura aura à 20 ans ? Pour aller dans l'autre sens (de la quantité d'eau au temps), il faut faire l'opération inverse: diviser par 30. \(\begin{matrix} temps \,(min) & \begin{matrix} ~ \xrightarrow[]{~~~\times 30~~~~~} ~\\ ~ \xleftarrow[~~~\div 30~~~~~]{} ~ \end{matrix} & quantit\acute e~d'~eau\,(L)\\ \end{matrix}\) Pour trouver le temps que l'on cherche, il faut donc faire: \(20\,000\,L \div 30\,L/min \approx 666,66 \,min \) Cette division ne s'arrête pas... Vous vous souvenez de l'astuce ? On reprend: \(20\,000\,L \div 30\,L/min = \frac{20\,000}{30} \,min \) On est bien avancés !!! Oui mais, si je mets cette fraction sur 60, j'obtiens des soixantièmes de minute: des secondes !!! \(20\,000\,L \div 30\,L/min = \frac{20\,000}{30} \,min = \frac{40\,000}{60} \,min = 40\,000 \,s\) Vous n'êtes toujours pas satisfaits ? (vous êtes durs...) finalement: \(40\,000 \,s = 666 \,min + 40 \,s = 11\,h + 6\,min + 40 \,s \) On remarque que 30 est le double de 15. Donc pour passer de la 2ème ligne à la 1ère, il suffit de multiplier par 2 (il faut 2 secondes pour faire couler 1L). En multipliant 20 000 par 2, on obtient 40 000. Il faut donc 40 000 secondes pour faire couler les 20 000L de la piscine. Et avec des divisions euclidiennes pour convertir des secondes en minutes et des minutes en heures: \(40\,000\,s = 666 \times 60\,s + 40\,s\) donc \(40\,000\,s = 666 \,min + 40\,s\) Finalement: \(40\,000 \,s = 666 \,min + 40 \,s = 11\,h + 6\,min + 40 \,s \) (suivant notre façon de voir les choses, on peut bien se raccourcir le travail...) Correction:
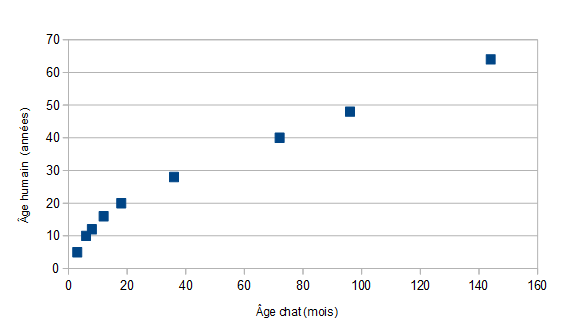
4 p94: âge en "années de chat"
Vérifier s'il y a un coefficient de proportionnalité
peut on trouver UN nombre par lequel multiplier la première ligne pour trouver la deuxième ligne ?
→ Il faut vérifier si on fait la même multiplication pour passer de 3 à 5, de 6 à 10, etc ... Vérifier que le tableau fonctionne bien avec les techniques que nous avons vu (celles avec l'exercice sur les crêpes)
Par exemple:
exemple: 6+12=18 mais est-ce que 10+16=20 ?? On peut aussi placer ces informations dans un graphique et voir si les nombres grandissent "avec la même régularité", mais vous verrez ça en 4ème
Ici, sans même faire de calcul, on pouvait remarquer qu'au début le nombre de l'âge humain (en années) est plus grand que le nombre de l'âge du chat (en mois) et qu'à la fin du tableau c'est l'inverse !
Cela ne convient pas avec une situation de proportionnalité car les nombres des deux lignes ne conservent pas la même proportion: la valeur de \(\frac{age~du~chat}{age~humain}\) change.
Âge du chat (mois)
3
6
8
12
18
36
72
96
144
Âge humain (ans)
5
10
12
16
20
28
40
48
64
rapport \(\frac{age~du~chat}{age~humain}\)
en fraction\(\frac{3}{5}\)
\(\frac{6}{10}\)
\(\frac{8}{12}\)
\(\frac{12}{16}\)
\(\frac{18}{20}\)
\(\frac{36}{28}\)
\(\frac{72}{40}\)
\(\frac{96}{48}\)
\(\frac{144}{64}\)
rapport \(\frac{age~du~chat}{age~humain}\)
en écriture décimale0,6
0,6
0,66666...
0,75
0,9
1,2857...
1,8
2
2,25
6 p94 âge et taille
Mais pour expliquer pourquoi... Eh bien c'est parce que la taille de Léa n'est pas proportionnelle à son âge: ce n'est donc pas parce que son âge aura doublé que ce sera la même chose pour sa taille. Heureusement !
Plus ou moins... mais pas par un simple calcul de proportionnalité en tout cas !
Sur votre carnet de santé, vous pouvez trouver des courbes qui permette d'estimer votre futur taille à partir de votre taille actuelle et de votre âge. Elles ont été construites à partir de statistiques (de très nombreuses données sur les enfants nés avant vous: leur taille, poids au cours du temps mais il faut aussi tenir compte de la taille des parents).
7 p94 l'exercice du robinet
Répondre à l'exercice revient à réussir à compléter ce tableau:
temps
30 secondes
??
quantité d'eau
15 L
20 000 L
Il s'agit bien d'un tableau de proportionnalité car comme le robinet est ouvert au maximum, il doit avoir un débit constant (cela veut dire qu'en une minute il coulera toujours la même quantité d'eau). Si on arrive a trouver combien d'eau sortent en 1 minute ("passage par l'unité"), il suffira de multiplier le nombre de minutes par ce nombre pour trouver la quantité d'eau totale. Si on arrive à trouver combien de temps il faut pour 1L, on pourra aussi s'en sortir (et bien plus vite...). Version longue: avec le coefficient de proportionnalité "du temps vers l'eau" et en mettant le temps en minutes:
Donc, si l'eau coule toujours avec le même débit, en 1 minute coulera 2 fois plus d'eau qu'en 30 secondes, soit 30L.
Le coefficient de proportionnalité (le nombre par lequel multiplier le nombre de minutes pour trouver le nombre de litres) est 30.
Eh bien sortons les divisions euclidiennes:
\(40\,000 = 60 \times 666 + 40\) donc 40 0000 secondes = 666 minutes + 40 secondes
\(666 = 60 \times 11 + 6\) donc 666 minutes = 11 heure + 6 minutes Version courte en laissant le temps en secondes et cherchant un coefficient de proportionnalité "de l'eau vers le temps":
\(666\,min = 11 \times 60\,min + 6\,min\) donc \(666\,min = 11 \,h + 6\,min\)
8 p95 prix des jeux videos 14 p96 pouls jus d'orange 15 p96 prix A faire: