
3èmes - Lundi 4 mai ~ jeudi 7 mai (3/3): évolution en pourcentage
Résumé de la séance:
- enchainement d'évolutions exprimées en pourcentages
Et non il n'y a pas d'erreur dans l'énoncé ! Une évolution de 15% suivie d'une de 20% ne revient pas à une évolution de 35% ! \(100€ \xrightarrow[+15€]{~~~~+15\% ~~~~} 115€ \xrightarrow[+23€]{~~~~+20\% ~~~~} 138€\) les 20% pour la 2ème augmentation se calculent sur 115€ (et non sur 100€), c'est pour ça que ça fait une augmentation de 23€ plutôt qu'une augmentation de 20€ \(prime~decembre \xrightarrow[]{~~~~+15\% ~~~~} prime~janvier \xrightarrow[]{~~~~+20\% ~~~~} prime~fevrier\) revient à: \(prime~decembre \xrightarrow[]{~~\times 1,15 ~~~~} prime~janvier \xrightarrow[]{~~\times 1,20 ~~~~} prime~fevrier\) et multiplier par 1,15 puis par 1,20 revient à multiplier en une fois par \((1,15 \times 1,20)\) soit 1,38. On obtient finalement: \( \begin{matrix} prime~decembre \xrightarrow[\times 1,15]{~~~~+15% ~~~~~} prime~janvier \xrightarrow[\times 1,20]{~~~~+20% ~~~~} prime~fevrier\\ Chloée fait une double erreur: Finalement: 15% de 5 points = \(5 \times 0,15 = 0,75\) 1. Au bout de 1 an, il touchera 2% d'intérêts, autrement dit 2% de ses 341,25€. On peut bien sûr aller plus vite avec: \(341,25 \times 1,02 = 348,075\) 2. Pour calculer la somme sur son compte au bout de 5 ans, on peut refaire ce calcul 5 fois de suite. On peut aussi gagner du temps ainsi: Finalement, au bout de 5 ans, il aura \(341,25 \times 1,02^5 \approx 341,25 \times 1,104 \approx 376,74\) Suivant la méthode d'arrondi appliqué chaque année, nous pouvons obtenir un résultat différent pour les centimes... \(341,25 \times 1,02^5 \approx 376,76757409...\) \(341,25 \times 1,104 = 376,74\) et Correction:
21 p145 calcul de prime
~~\xrightarrow[+38\%]{~~~~~~~~~~~~~~~~~~~~~~~~\times 1,38~~~~~~~~~~~~~~~~~~~~~~~~~}{~}
~\end{matrix} \) 22 p145 Correction d'une erreur d'interprétation
quand on dit "augmenter de 15%" on veut en fait dire "augmenter de 15% du nombre de départ"
Elle s'engage donc à améliorer sa moyenne de 0,75 points, ce qui l'amènerait à 5,75/20... On est loin du 20/20 !!! 27 p145 compte en banque et taux d'intérêt
\(341,25 \times 2\% = 341,25 \times 0,02 = 6,825\)
Il aura donc \(341,25 + 6,825 = 348,075\) (la banque arrondira à 348,07€).
En faisant bien attention ! Il ne gagnera pas 6,82€ tous les ans car la 2ème année il touchera 2% de 348,07€.
Ainsi, ses intérêts augmenteront tous les ans.
multiplier 5 fois de suite par 1,02 revient à multiplier en une fois par \(1,02^5\) autrement dit par 1,104 environ.
On peut remarquer que cela ne revient pas à une augmentation de 10% mais d'un peu plus.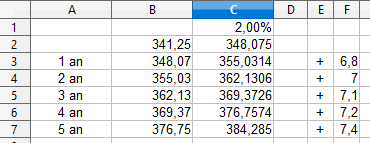
détails
(vous vous rappelez de l'intérêt du "$" ?)
On peut remarquer que l'erreur qu'il ne fallait surtout pas faire au 21 p145 est moins grave dans le 27 p145:
\(evolution~de~ 20\% ~suivie ~d'une~ de~ 15\% ~\neq evolution ~de~ (20\%+15\%) \)
alors que
\(5~ evolutions~successives~ de ~2\% ~\approx ~evolution ~de ~(5\times2\%)\)
En fait, plus les taux d'évolution sont faibles et moins cette erreur d'additionner les taux d'évolution est grave:
~~\xrightarrow[\approx +3\%]{~~~~~~~~~~~~~~~~~~~~~~~~\times 1,302~~~~~~~~~~~~~~~~~~~~~~~~~}{~}
~\end{matrix} \)
~~\xrightarrow[+140\% ~~!!!]{~~~~~~~~~~~~~~~~~~~~~~~~\times 2,4~~~~~~~~~~~~~~~~~~~~~~~~~}{~}
~\end{matrix} \)
Voyons voir si tout cela est bien passé:
23 p145 augmentation à la boulangerie exercice: Un magasin peut scrupuleux augmente ses prix de 20% un mois avant les soldes. Le jour des soldes, il affiche une pancarte "TOUT à -20% !". 48 p149 calculs avec des % (se référer aux explications de début de chapitre si nécessaire) A faire:
Qu'en pensez vous ?



