3èmes - Lundi 4 mai ~ jeudi 7 mai (2/3): évolution en pourcentage
Résumé de la séance:
- appliquer une évolution exprimée en pourcentage en utilisant une multiplication
Correction:
D'après ce qu'on a vu à la séance précédente:
1. Augmenter une quantité de 30% revient à la multiplier par \(1+30\%\) et \(1+30\% = 1+0,30 = 1,30\).
explications:
- la quantité de départ représente 100%
- si on lui rajoute 30% d'elle même, il est normal d'obtenir 130% de cette quantité de départ
- donc pour calculer la nouvelle quantité, on peut calculer 130% de la quantité de départ
et cela se fait ainsi: \(quantité~de~depart \times 130\%\) - mais d'où viennent ce 1 et ce 0,30 ?
\(1 = \frac{100}{100}=100\%\) et \(0,30 = \frac{30}{100}=30\%\)
2. Diminuer une quantité de 5% revient à la multiplier par \(1-5\%\) et \(1-5\% = 1-0,05 = 0,95\).
(on obtient donc à la fin 95% du résultat de départ)
3. Multipler une quantité par 1,6 revient à l'augmenter de 60%.
Si la nouvelle quantité représente 160% de celle de départ, c'est qu'on a augmenté de 60%.
Calculs: \(1,6 -1 = 0,60 = 60\%\) ( \(1,6 -1\) revient au même que \(160\% - 100\%\))
4. Multipler une quantité par 0,85 revient à la diminuer de 15%.
Calculs: \(0,85 -1 = -0,15 = -15\%\)
( ou encore \(0,85=85\%\) , on a donc "perdu" 15% par rapport aux 100% de départ: \(85\% - 100\% = -15\%\))
| Ancien prix | baisse de ... | multiplier l'ancien prix par ... | nouveau prix |
| 40€ | 30% | 0,7 | 28€ |
| 260€ | 20% | 0,8 | 208€ |
| 89,50€ | 10% | 0,9 | 80,55€ |
| 11,20€ | 5% | 0,95 | 10,64€ |
Le 0,7 a été obtenu avec \(100\% - 30\% = 1-0,30 = 0,70\) (bref 70%).
On obtient de même:
\(1-0,20 = 0,80\) (baisse de 20% → nouveau prix = 80% du prix de départ)
\(1-0,10 = 0,90\) (baisse de 10% → nouveau prix = 90% du prix de départ)
\(1-0,005 = 0,95\) (baisse de 5% → nouveau prix = 95% du prix de départ)
Bien sûr, l'idée d'utiliser une multiplcation par 0.7, 0.8 au encore 0.95 est de prendre la calculatrice ou d'utiliser un logiciel tableur par exemple, mais par principe:
- le 28€ peut se calculer mentalement avec \(4\times7 = 28\) ( \(40 \times 0,7 = 4 \times 10 \times 7 \div 10\) ...)
- le 208€ peut se calculer mentalement ainsi:
10% de 260€ = 26€ donc 20% de 260€ = 52€ puis 260€-52€ - 10% de 89,50€ = 8,95€ puis 89,50€-8,95€=80,55€
- 10% de 11,20€ = 1,12€ donc 5% de 11,20€ = 0,56€ puis 11,20€-0,56€=10,64€
Mais pourquoi utiliser cette méthode alors qu'on en avait d'autres avant ?
- 1ere réponse: comme je vient de l'évoquer juste au dessus, pour effectuer les calculs avec une machine
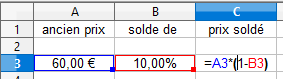
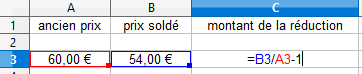
calcul d'un prix soldécalcul d'un taux d'évolution - 2ème réponse: pour mieux comprendre ce qui se passe quand on enchaine les évolutions, voyons cela...
A faire:
21 p145 calcul de prime (bizarre cet énoncé...)
Conseil: essayez sur un exemple simple, par exemple une prime de départ de 100€
22 p145 Correction d'une erreur d'interprétation
27 p145 compte en banque et taux d'intérêt