
5ème N5 Proportionnalité - échelle
Lorsqu'on veut représenter quelque chose de trop grand ou de trop petit à une taille qui nous convient, on utilise la notion d'échelle. Cela consiste à conserver la forme réelle mais pas la taille.
Exemples:
- un carte, un plan
- une maquette
- une photographie prise au microscope ou depuis un satellite
- etc ...
L'échelle est l'information qui nous permet de connaître la longueur réelle représentée à partir d'une mesure sur la représentation.
Quelques exemples d'échelles utilisées pour des maquettes
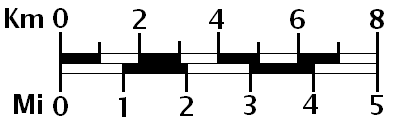
Exemples de représentations d'une échelle sur une carte:
By Anna Frodesiak - Own work, CC0, Link
By Eric Gaba (Sting - fr:Sting) - Own work, Public Domain, Link
Entrons un peu dans les détails, une échelle est souvent donnée par une fraction:
\( échelle = \frac{distance ~de ~la~ représentation}{distance~ réelle~ représentée} \)
Imaginons une carte où 1 cm représente 1 km, dans ce cas:
\( échelle = \frac{distance ~de ~la~ représentation}{distance~ réelle~ représentée} = \frac{1\, cm}{1\, km} = \frac{1 \,cm}{100\, 000\, cm} = \frac{1}{100 \,000} \)
L'échelle de cette carte est 1/100 000.
Autrement dit:
- la représentation représente 1/100 000 de la réalité
- quelque chose dessiné sur la carte est 100 000 fois plus petit que la réalité
- pour parcourir une certaine distance sur la carte, il faut en parcourir une 100 000 fois plus grande dans la réalité
Inversement, sur une carte à l'échelle 1/25 000 (c'est le cas des fameuses cartes IGN):
\( \frac{1}{25 \,000} = \frac{1\, cm}{25\,000 \,cm} = \frac{1\, cm}{250 \,m} \)
donc sur une carte à l'échelle 1/25 000, 1 cm représente 250 m.
Voici en image quelques repères sur l'échelle des cartes classiques:

prélevé dans la brochure Découvrez le monde des cartes sur le site http://education.ign.fr
Pour compléter, vous pourrez trouver des brochures intéressantes sur http://education.ign.fr/dossiers/lire-une-carte-et-sorienter parmi lesquelles:
- Mesurer les distances avec une carte (fiche 5) → exemples de calculs
- Lire et utiliser une carte (fiche 1) → choisir une carte


